4. Basic Data Structures for Analysis: NumPy

1. Introduction to NumPy

2. Difference with list

3. Basics of Numpy

4. Mathematical Operations

5. Accesing Arrays

6. Statistical Measures

7. Basic Linear Algebra in NumPy

4.1. Introduction to NumPy

• NumPy (pronounced "numb pie") is one of the most important packages to grasp when you’re starting to learn Python

• The package is known for a very useful data structure called the NumPy array. NumPy also allows Python developers to quickly perform a wide variety of numerical computations.

• The main benefit of NumPy is that it allows for extremely fast data generation and handling. NumPy has its own built-in data structure called an array which is similar to the normal Python list, but can store and operate on data much more efficiently

• It also has functions for working in domain of linear algebra, fourier transform, and matrices.

“NumPy is the fundamental package for scientific computing with Python. It contains among other things:

a powerful N-dimensional array object sophisticated (broadcasting) functions tools for integrating C/C++ and Fortran code useful linear algebra, Fourier transform, and random number capabilities Besides its obvious scientific uses, NumPy can also be used as an efficient multi-dimensional container of generic data. Arbitrary data-types can be defined. This allows NumPy to seamlessly and speedily integrate with a wide variety of databases.

NumPy is licensed under the BSD license, enabling reuse with few restrictions.”

4.1.1. Data Structures in Linear Algebra

There are different types of objects (or structures) in linear algebra and as corollary in NumPy:

• Scalar: Single number
• Vector: 1-D Array of numbers
• Matrix: 2-dimensional array of numbers
• Tensor: N-dimensional array of numbers where n > 2

4.1.2. Difference with list

• In Python we have lists that may serve the purpose of arrays, but they are slow to process.

• NumPy aims to provide an array object that is up to 50x faster that traditional Python lists.

• The array object in NumPy is called ndarray, it provides supporting functions that make working with ndarray easy.

• Arrays are frequently used in data science, where speed and resources are very important.

• NumPy arrays are stored at one continuous location in memory unlike lists, so programs can access and manipulate them more efficiently.

• This behavior is called locality of reference in computer science.

• This is the reason why NumPy is faster than lists. Also it is optimized to work with latest CPU architectures

4.2 Basics of Numpy

import numpy as np

#!pip install numpy --upgrade

print(np.__version__)

1.19.5

!pip show numpy

Name: numpy
Version: 1.20.1
Summary: NumPy is the fundamental package for array computing with Python.
Home-page: https://www.numpy.org
Author: Travis E. Oliphant et al.
Author-email: None
License: BSD
Location: /usr/local/lib/python3.7/dist-packages
Requires: 
Required-by: yellowbrick, xgboost, xarray, wordcloud, umap-learn, torchvision, torchtext, torch, tifffile, thinc, Theano, tensorflow, tensorflow-probability, tensorflow-hub, tensorflow-datasets, tensorboard, tables, statsmodels, spacy, sklearn-pandas, seaborn, scs, scipy, scikit-learn, resampy, qdldl, PyWavelets, python-louvain, pystan, pysndfile, pymc3, pyemd, pyarrow, plotnine, patsy, pandas, osqp, opt-einsum, opencv-python, opencv-contrib-python, numexpr, numba, np-utils, nibabel, moviepy, mlxtend, mizani, missingno, matplotlib, matplotlib-venn, lucid, lightgbm, librosa, knnimpute, Keras, Keras-Preprocessing, kapre, jpeg4py, jaxlib, jax, imgaug, imbalanced-learn, imageio, hyperopt, holoviews, h5py, gym, gensim, folium, fix-yahoo-finance, fbprophet, fastprogress, fastdtw, fastai, fancyimpute, fa2, ecos, daft, cvxpy, cufflinks, cmdstanpy, chainer, Bottleneck, bokeh, blis, autograd, atari-py, astropy, altair, albumentations

4.2.1 Creating numpy array

💡

4.2.1.1 np.array to define array

• The following are examples of creating numpy array from list
• This is a natural progression in being able to handle large volumes of data

arr = np.array([1, 2, 3, 4, 5])
print(arr)
print(type(arr))

[1 2 3 4 5]
<class 'numpy.ndarray'>

# dtype parameter 
a = np.array([1, 2, 3, 4.444], dtype = float) 
print (a)

[1.    2.    3.    4.444]

4.2.1.2 np.asarray to define array

• np.array() creates a copy of the object array and would not reflect changes to the original array with default parameters
• np.asarray() changes the original variable

# convert list to ndarray 
x = [1,2,3] 
a = np.asarray(x) 
print (a)

# dtype is set 
a = np.asarray(x, dtype = float) 
print (a)

# ndarray from tuple 
x = (1,2,3) 
a = np.asarray(x) 
print (a)

# ndarray from list of tuples 
x = [(1,2,3),(4,5, np.nan)] 
a = np.asarray(x) 
print (a)

[1 2 3]
[1. 2. 3.]
[1 2 3]
[[ 1.  2.  3.]
 [ 4.  5. nan]]

4.2.1.3. Using np.linespace

numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None, axis=0) function returns evenly spaced numbers over a specified interval

• start and stop — required arguments.
• The number of samples generated is specified by the third argument num. If omitted, 50 samples are generated.
• One important thing to bear in mind while working with this function is that the stop element is provided in the returned array (by default endpoint=True)
• np.arange is a similar function but doesn't allow you to define the endpoint

# Linspace function

# array with 11 elements, last element included
np.linspace(0,10)

array([ 0.        ,  0.20408163,  0.40816327,  0.6122449 ,  0.81632653,
        1.02040816,  1.2244898 ,  1.42857143,  1.63265306,  1.83673469,
        2.04081633,  2.24489796,  2.44897959,  2.65306122,  2.85714286,
        3.06122449,  3.26530612,  3.46938776,  3.67346939,  3.87755102,
        4.08163265,  4.28571429,  4.48979592,  4.69387755,  4.89795918,
        5.10204082,  5.30612245,  5.51020408,  5.71428571,  5.91836735,
        6.12244898,  6.32653061,  6.53061224,  6.73469388,  6.93877551,
        7.14285714,  7.34693878,  7.55102041,  7.75510204,  7.95918367,
        8.16326531,  8.36734694,  8.57142857,  8.7755102 ,  8.97959184,
        9.18367347,  9.3877551 ,  9.59183673,  9.79591837, 10.        ])

# array with 11 elements, last element not included
np.linspace(0,10,11,endpoint=False)

array([0.        , 0.90909091, 1.81818182, 2.72727273, 3.63636364,
       4.54545455, 5.45454545, 6.36363636, 7.27272727, 8.18181818,
       9.09090909])

Linspace function can be used to generate evenly spaced samples along a axis.

4.2.1.4. Using np.ones, np.zeros, np.repeat

💡

rows=5
columns=1
z= np.zeros((rows,columns))
print(z)

[[0.]
 [0.]
 [0.]
 [0.]
 [0.]]

rows=1
columns=5
o= np.ones((rows,columns))
print(o)

[[1. 1. 1. 1. 1.]]

repeats=5
r= np.repeat(3, repeats)
print(r)

[3 3 3 3 3]

4.2.2 Dimensions in array

4.2.2.1 1-Dimensional array: Often called a vector

A vector can be row or a column vector

import numpy as np

arr = np.array([1, 2, 3, 4, 5])
print(arr)
print('rows and columns:',arr.shape)
print('length:', len(arr))

[1 2 3 4 5]
rows and columns: (5,)
length: 5

col = np.array([[1],[2],[3],[4],[5]])
print(col)
print('rows and columns:',col.shape)
print('length:', len(col))

[[1]
 [2]
 [3]
 [4]
 [5]]
rows and columns: (5, 1)
length: 5

Array with dimension (5,) is a flat array (1D array) of 5 items, where as (5, 1) is matrix (2D array) with 1 column and 5 rows

4.2.2.2. 2 Dimensional array: Often called a 2 D Matrix

import numpy as np

arr2d = np.array([[1, 2, 3], [4, 5, 6]])

print(arr2d)
print('rows x columns',arr2d.shape)
print('length:', len(arr2d))

[[1 2 3]
 [4 5 6]]
rows x columns (2, 3)
length: 2

4.2.2.3. 3-Dimensional Array

import numpy as np

arr = np.array([[[1, 2, 3], [4, 5, 6]], [[1, 2, 3], [4, 5, 6]]])

print(arr)
print('stacks x rows x columns:',arr.shape)

[[[1 2 3]
  [4 5 6]]

 [[1 2 3]
  [4 5 6]]]
stacks x rows x columns: (2, 2, 3)

Every heard of Tensorflow?

A tensor is an algebraic object that describes a (multilinear) relationship between sets of algebraic objects related to a vector space.

4.2.3. np.reshape Reshaping numpy array

• Reshaping means changing the shape of an array.

• The shape of an array is the number of elements in each dimension.

• By reshaping we can add or remove dimensions or change number of elements in each dimension.

print(arr2d)
print(arr2d.shape)
arr_new = arr2d.reshape(1,6)
print(arr_new)
print(arr_new.shape)

[[1 2 3]
 [4 5 6]]
(2, 3)
[[1 2 3 4 5 6]]
(1, 6)

Observe above that the total number of elements remain the same

Reshape can be used while declaring an array

new = np.linspace(0,9,9).reshape(3,3)
print(new)
print(new.shape)

[[0.    1.125 2.25 ]
 [3.375 4.5   5.625]
 [6.75  7.875 9.   ]]
(3, 3)

4.2.3.1 Reshaping numpy array with a unknown parameter

💡

• The criterion to satisfy for providing the new shape is that 'The new shape should be compatible with the original shape'
• numpy allow us to give one of new shape dimension as -1.
• It simply means that we want numpy to figure this out.
• numpy will do so by looking at the 'length of the array and remaining dimensions' and making sure new and earlier shapes are compatible

z = np.array([[1, 2, 3, 4],
         [5, 6, 7, 8],
         [9, 10, 11, 12]])
print('~~ Input Matrix ~~')
print(z)
print('rows x columns:', z.shape)
print()
print('~~ Ex1. Flat Array ~~')
print('Give me a flat array without specifying the length')
print(z.reshape(-1))
print('length:', z.reshape(-1).shape)
print()
print('~~ Ex2. Single Dimension ~~')
print('Give me a single dimensional array')
print(z.reshape(-1,1))
print('length:', z.reshape(-1,1).shape)
print()
print('~~ Ex3. 2 Column ~~')
print('Give me a 2 column array and figure out the number of rows')
print(z.reshape(-1,2))
print('length:', z.reshape(-1,2).shape)

~~ Input Matrix ~~
[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]
rows x columns: (3, 4)

~~ Ex1. Flat Array ~~
Give me a flat array without specifying the length
[ 1  2  3  4  5  6  7  8  9 10 11 12]
length: (12,)

~~ Ex2. Single Dimension ~~
Give me a single dimensional array
[[ 1]
 [ 2]
 [ 3]
 [ 4]
 [ 5]
 [ 6]
 [ 7]
 [ 8]
 [ 9]
 [10]
 [11]
 [12]]
length: (12, 1)

~~ Ex3. 2 Column ~~
Give me a 2 column array and figure out the number of rows
[[ 1  2]
 [ 3  4]
 [ 5  6]
 [ 7  8]
 [ 9 10]
 [11 12]]
length: (6, 2)

4.2.4 Combining and Spliting

4.2.4.1. np.concatenate()

💡

cust_id = [1,2,3,4,5]
cc_bal= [200, 3000, 3500, 4000, 50]
cc_score= [700, 630, 600, 590, 780]
print('customer', cust_id,'\n' ,'credit card balance:',cc_bal,'\n' , 'credit score:', cc_score)
print()
print('Convert to flat Array:')
cust_id= np.asarray(cust_id)
cc_bal= np.asarray(cc_bal)
cc_score= np.asarray(cc_score)
print('cust shape:', cust_id.shape, 'cc_bal shape:', cc_bal.shape,\
      'cc_Score shape:', cc_score.shape)
print()
print('Convert to Single Dimension Array (column vector):')
cust_id= cust_id.reshape(-1,1)
cc_bal= cc_bal.reshape(-1,1)
cc_score= cc_score.reshape(-1,1)
print('cust shape:', cust_id.shape, 'cc_bal shape:', cc_bal.shape,\
      'cc_Score shape:', cc_score.shape)
print()
print('Concatenate into single nxm array')
all_cust= np.concatenate((cust_id, cc_bal, cc_score),axis=1)
print(all_cust)
print('Shape:', all_cust.shape)
print()

customer [1, 2, 3, 4, 5] 
 credit card balance: [200, 3000, 3500, 4000, 50] 
 credit score: [700, 630, 600, 590, 780]

Convert to flat Array:
cust shape: (5,) cc_bal shape: (5,) cc_Score shape: (5,)

Convert to Single Dimension Array (column vector):
cust shape: (5, 1) cc_bal shape: (5, 1) cc_Score shape: (5, 1)

Concatenate into single nxm array
[[   1  200  700]
 [   2 3000  630]
 [   3 3500  600]
 [   4 4000  590]
 [   5   50  780]]
Shape: (5, 3)

4.2.4.2. np.split()

np.split(array, indices_or_sections, axis)

• indices_or_sections: Can be an integer, indicating the number of equal sized subarrays to be created from the input array. If this parameter is a 1-D array, the entries indicate the points at which a new subarray is to be created.
• axis defaults to 0

cust_id, cc_bal, cc_score= np.split(all_cust, 3, axis=1)
print('customer', '\n' ,cust_id,'\n' ,'credit card balance:','\n' ,cc_bal,'\n' , 'credit score:', '\n' ,cc_score)
print()
for i in range(all_cust.shape[0]):
  print('Customer Num:',i,np.split(all_cust, all_cust.shape[0], axis=0)[i])

customer 
 [[1]
 [2]
 [3]
 [4]
 [5]] 
 credit card balance: 
 [[ 200]
 [3000]
 [3500]
 [4000]
 [  50]] 
 credit score: 
 [[700]
 [630]
 [600]
 [590]
 [780]]

Customer Num: 0 [[  1 200 700]]
Customer Num: 1 [[   2 3000  630]]
Customer Num: 2 [[   3 3500  600]]
Customer Num: 3 [[   4 4000  590]]
Customer Num: 4 [[  5  50 780]]

4.3. Mathematical Operations

4.3.1. Simple Arithmetic functions

Numpy has special reserved methods for performing operations on numpy objects

4.3.1.1. `np.add()`, `np.subtract()`, `np.multiply()`, `np.divide()`

💡

a = np.linspace(0,8,9, dtype='float')
print(a)
a = np.linspace(0,8,9, dtype = np.float).reshape(3,3) 

print ('First array:') 
print (a) 

print ('Second array:') 
b = np.array([10,5,1]) 
print (b) 

print ('Add the two arrays:') 
print (np.add(a,b))

print ('Subtract the two arrays:') 
print (np.subtract(a,b)) 

print ('Multiply the two arrays:') 
print (np.multiply(a,b)) 

print ('Divide the two arrays:') 
print (np.divide(a,b))

[0. 1. 2. 3. 4. 5. 6. 7. 8.]
First array:
[[0. 1. 2.]
 [3. 4. 5.]
 [6. 7. 8.]]
Second array:
[10  5  1]
Add the two arrays:
[[10.  6.  3.]
 [13.  9.  6.]
 [16. 12.  9.]]
Subtract the two arrays:
[[-10.  -4.   1.]
 [ -7.  -1.   4.]
 [ -4.   2.   7.]]
Multiply the two arrays:
[[ 0.  5.  2.]
 [30. 20.  5.]
 [60. 35.  8.]]
Divide the two arrays:
[[0.  0.2 2. ]
 [0.3 0.8 5. ]
 [0.6 1.4 8. ]]

4.3.1.2. Reciprocal

• Reciprocal isn't the same as inverse of a array
• It replaces every entry in the array with 1/entry

a = np.array([0.25, 1.33, 1, 0, 100]) 

print ('Our array is:') 
print (a) 

print ('After applying reciprocal function:') 
print (np.reciprocal(a)) 

Our array is:
[  0.25   1.33   1.     0.   100.  ]
After applying reciprocal function:
[4.        0.7518797 1.              inf 0.01     ]

/usr/local/lib/python3.7/dist-packages/ipykernel_launcher.py:7: RuntimeWarning: divide by zero encountered in reciprocal
  import sys

4.3.1.3. Extensive Support

Note: Few other importtant functions that I won't cover but you should check them out are as follows:

• np.power()
• np.around()
• np.ceil()
• np.floor()

Numpy supports most arithematic function on arrrays that are applicable to numbers

4.3.1.4. Scalar Operations

const=3
print('Original Array:')
print(a)
print('Adding a Scalar')
print(a+const)
print('Substracting a Scalar')
print(a-const)
print('Multiply a Scalar')
print(a*const)
print('Div by a Scalar')
print(a/const)

Original Array:
[  0.25   1.33   1.     0.   100.  ]
Adding a Scalar
[  3.25   4.33   4.     3.   103.  ]
Substracting a Scalar
[-2.75 -1.67 -2.   -3.   97.  ]
Multiply a Scalar
[  0.75   3.99   3.     0.   300.  ]
Div by a Scalar
[ 0.08333333  0.44333333  0.33333333  0.         33.33333333]

4.4. Accessing Arrays

4.4.1 Accessing 1-D Array

import numpy as np

arr = np.array([1, 2, 3, 4])

print(arr[3])

4

4.4.2 Accessing 2-D Array

import numpy as np

arr = np.array([[1,2,3,4,5], [6,7,8,9,10]])
print(arr)
print('5th element on 2nd dim: ', arr[1, 4])

[[ 1  2  3  4  5]
 [ 6  7  8  9 10]]
5th element on 2nd dim:  10

Watch Out:- Python indexing always starts at 0

4.4.3 Accessing 3-D Array

import numpy as np

arr = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])
print(arr)
print()
print('Shape: ', arr.shape)
print()
print('0th stack, 1st row, 2nd column:', arr[0,1,2])
print('1st stack, 1st row, 1st column:', arr[1,1,1])

[[[ 1  2  3]
  [ 4  5  6]]

 [[ 7  8  9]
  [10 11 12]]]

Shape:  (2, 2, 3)

0th stack, 1st row, 2nd column: 6
1st stack, 1st row, 1st column: 11

4.4.4 Boolean Indexing

names = np.array(['New York', 'Los Angeles', 'Chicago','Houston','Phoenix'])

print(names == "Chicago")

[False False  True False False]

Watch Out:- Testing for equality is == and not = which is assignment in Python

print(names[names=='Los Angeles'])

['Los Angeles']

print(names)

['New York' 'Los Angeles' 'Chicago' 'Houston' 'Phoenix']

• In the code the index where the logical statement is True will be used to fetch the row having the same index in the array data.
• As if the row of data is actually for San Francisco

population =np.array([8.34, 3.98, 2.69, 2.32, 1.68]) # approx in millions
area= np.array([301.5, 468.7, 227.3, 637.5, 517.6]) # Square Miles

data= np.concatenate((population,area), axis=0).reshape(2,5)

data

array([[  8.34,   3.98,   2.69,   2.32,   1.68],
       [301.5 , 468.7 , 227.3 , 637.5 , 517.6 ]])

b= names=='Los Angeles'
print('Select the Column Index')
print(b)
print('Repeat and select the rows and columns you want to select')
slc= np.concatenate([[b]] * 2, axis=0)
print(slc)
print('Slice by the selection')
print(data[slc])

Select the Column Index
[False  True False False False]
Repeat and select the rows and columns you want to select
[[False  True False False False]
 [False  True False False False]]
Slice by the selection
[  3.98 468.7 ]

function slice requires three paramters (start,stop,step)

a = np.arange(10,21,1)
print(a)
print(a.shape)
s = slice(2,7,2) # (start-2,stop-7,step-2)
print(s)
print (a[s])

[10 11 12 13 14 15 16 17 18 19 20]
(11,)
slice(2, 7, 2)
[12 14 16]

b = a[2:7:2] # [Start:Stop:Step]
print (b)

# slice single item 
a = np.arange(10) 
b = a[5] 
print (b)

[12 14 16]
5

# slice items starting from index 
a = np.arange(0,10,10) 
print (a[2:])

a = np.array([[1,2,3],[4,5,6],[7,8,9]]) 
print (a)  

[]
[[1 2 3]
 [4 5 6]
 [7 8 9]]

# slice items starting from index
print ('Now we will slice the array from the index a[1:]') 
print(a)
print (a[1:])
print (a[1][1])
print (a[1][1:])

Now we will slice the array from the index a[1:]
[[1 2 3]
 [4 5 6]
 [7 8 9]]
[[4 5 6]
 [7 8 9]]
5
[5 6]

# this returns array of items in the second column 
print ('The items in the second column are:')  
print (a[...,1]) 

The items in the second column are:
11

# Now we will slice all items from the second row 
print ('The items in the second row are:') 
print (a[1,...]) 

The items in the second row are:
[4 5 6]

# Now we will slice all items from column 1 onwards 
print ('The items column 1 onwards are:') 
print (a[...,1:])

The items column 1 onwards are:
[[2 3]
 [5 6]
 [8 9]]

4.6. Numpy: Statistical measures

4.6.1 Percentile

Given a vector V of length N, the q-th percentile of V is the value q/100 of the way from the minimum to the maximum in a sorted copy of V.

import numpy as np 
a = np.array([[30,40,70],[80,20,10],[50,90,60],[100,120,150]]) 

print( 'Our array is:') 
print (a) 
print ('\n')  

print ('Applying percentile() function:') 
print( np.percentile(a,50)) 
print ('\n'  )

print ('Applying percentile() function along axis 1:') 
print( np.percentile(a,50, axis = 1) )
print ('\n' ) 

print ('Applying percentile() function along axis 0:' )
print (np.percentile(a,75, axis = 0))

Our array is:
[[ 30  40  70]
 [ 80  20  10]
 [ 50  90  60]
 [100 120 150]]


Applying percentile() function:
65.0


Applying percentile() function along axis 1:
[ 40.  20.  60. 120.]


Applying percentile() function along axis 0:
[85.  97.5 90. ]

4.6.2 Other Statistical Functions

• np.median(): Given a vector V of length N, the median of V is the middle value of a sorted copy of V, V_sorted - i e., V_sorted[(N-1)/2], when N is odd, and the average of the two middle values of V_sorted when N is even.
• np.mean(): Returns the average of the array elements. The average is taken over the flattened array by default, otherwise over the specified axis.
• np.std(): Returns the standard deviation, a measure of the spread of a distribution, of the array elements. The standard deviation is computed for the flattened array by default, otherwise over the specified axis.
• np.var(): Returns the variance of the array elements, a measure of the spread of a distribution. The variance is computed for the flattened array by default, otherwise over the specified axis.

4.6.3 np.argmax()

The numpy.argmax(a, axis=None, out=None)function returns the indices of the maximum values along an axis. In a 2d array, we can easily obtain the index of the maximum value as follows:

print(all_cust)
print()
print('Row with the Highest Value for each column:')
np.argmax(all_cust, axis=0)

[[   1  200  700]
 [   2 3000  630]
 [   3 3500  600]
 [   4 4000  590]
 [   5   50  780]]

Row with the Highest Value for each column:

array([4, 3, 4])

4.6.4 np.histogram()

The numpy.histogram(a, bins=10, range=None, normed=None, weights=None, density=None)computes the histogram of a set of data. The function returns 2 values: (1) the frequency count, and (2) the bin edges

np.histogram(cc_bal,bins=10)

(array([2, 0, 0, 0, 0, 0, 0, 1, 1, 1]),
 array([  50.,  445.,  840., 1235., 1630., 2025., 2420., 2815., 3210.,
        3605., 4000.]))

4.6.5 np.randint()

4.7 Basic Linear Algebra in NumPy

💡💡

4.7.1. Meet the eye

Identity matrix is a square matrix whose diagonal values are all 1. NumPy has a built-in function called eye that takes in one argument for building identity matrices.italicized text

print('1x1 Identity Matrix','\n',np.eye(1))
print()
#Returns a 1x1 identity matrix

print('5x5 Identity Matrix','\n',np.eye(5)) 
#Returns a 5x5 identity matrix

1x1 Identity Matrix 
 [[1.]]

5x5 Identity Matrix 
 [[1. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0.]
 [0. 0. 1. 0. 0.]
 [0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 1.]]

4.7.2. The dot Product

💡

• The dot product of two vectors is the sum of the products of elements with regards to position. The first element of one vector is multiplied by the first element of the second vector and so on.
• The sum of these products is the dot product which can be done with np.dot() function
• Usually denoted as v1.v2. Vectors need to be of same length for successful multiplication

v1= np.array([1,2,3])
v2= np.array([1,1,2])
print(np.dot(v1,v2))
v2= np.array([1,1,3,2])
if len(v1)== len(v2):
  print(np.dot(v1,v2))
else:
  print('Dot product will fail: Vectors not of same length')

9
Dot product will fail: Vectors not of same length

4.7.3. Matrix Multiplication

• Remember a 2 D Array is a Matrix
• Matrix multiplication of two matrices is based on dot products of rows of one matrix with the columns of other matrix. Each element of the product matrix is a dot product of a row in first matrix and a column in the second matrix.
• Number of columns in the 1st matrix needs to have same number of rows in the 2nd matrix If M= A*B. And A is size nxk and B is kxm. The final size of M is nxm

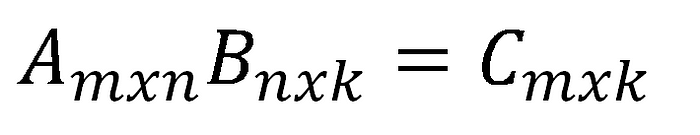
A1= np.random.randint(5, size=(3,2))
print(A1)
A2= np.random.randint(5, size=(2,5))
print(A2)

[[3 1]
 [2 0]
 [3 0]]
[[0 2 3 1 0]
 [2 0 2 0 0]]

m= np.matmul(A1, A2)
print(m)

[[ 2  6 11  3  0]
 [ 0  4  6  2  0]
 [ 0  6  9  3  0]]

4.7.4. np.transpose()

Reverse or permute the axes of an array; returns the modified array.

For an array a with two axes, transpose(a) gives the matrix transpose.

print()
print(m)
print(m.shape)
print()
print('Matrix Transpose')
print(m.T)
print(m.T.shape)

[[ 2  6 11  3  0]
 [ 0  4  6  2  0]
 [ 0  6  9  3  0]]
(3, 5)

Matrix Transpose
[[ 2  0  0]
 [ 6  4  6]
 [11  6  9]
 [ 3  2  3]
 [ 0  0  0]]
(5, 3)

4.7.5. np.linalg.inv()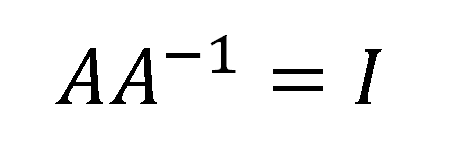

💡

• The inverse of a matrix is such that if it is multiplied by the original matrix, it results in identity matrix

• Not all matrix are invertible. The way to test is for a finite condition number as in numpy.isfinite(numpy.linalg.cond(A))== True

import numpy as np
x = np.array([[1,2],[3,4]]) 
# Watch out!! The inverse is called as np.linalg and not just np
y = np.linalg.inv(x) 
print(x) 
print(y) 
print(np.dot(x,y))

[[1 2]
 [3 4]]
[[-2.   1. ]
 [ 1.5 -0.5]]
[[1.0000000e+00 0.0000000e+00]
 [8.8817842e-16 1.0000000e+00]]